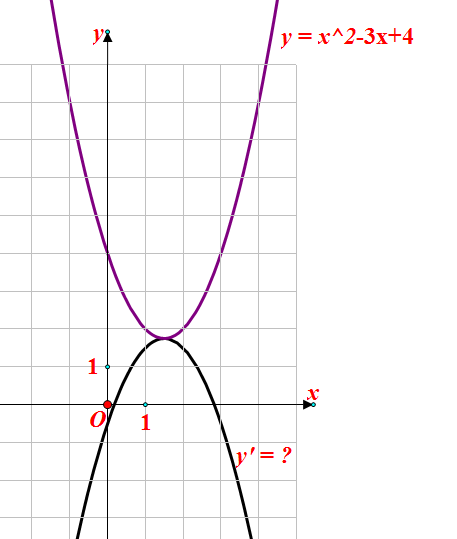
题目:已知二次函数y=x^2-3x+4的图像如图。将函数图像绕其顶点旋转180度后得到新的图像,求新的图像的解析式。
思路与分析:
1、二次函数的图像为一抛物线。区别平面直角坐标系中的不同抛物线,一是“形状”--也即是抛物线的开口方向和开口大小,二是抛物线的“位置”--也就是顶点坐标。
2、在二次函数y=ax^2+bx+c的系数a、b、c中,a决定图像的开口方向和开口大小,a、b、c共同决定图像顶点的坐标。
3、题目中两条抛物线,其开口方向不同,开口大小相同,顶点坐标相同,我们可利用这些关系解答本题
解:设函数y=x^2-3x+4的顶点坐标为(a,b),则
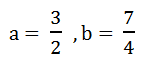
(* 直接代入二次函数顶点坐标公式计算即可)
∵ 待求的函数,图像与原函数图像顶点相同
∴ 待求的函数可以写作:
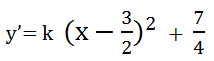
两个函数图像的顶点相同
又∵ 待求的函数,图像与原函数图像开口大小相同,开口方向相反
∴ k=-1
即待求的函数为:
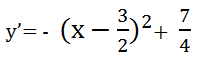
两个函数图像的开口方向相反,开口大小相同
或写作:
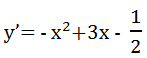
最好保留成“一般式”的形式
