一、前言(废话)
我们已经学习了高中阶段的指数函数,对数函数,幂函数,以及相关的性质。但是只学习了函数是不够的,还有很多知识点是需要学习的,万里征程只走了一小步,今天作者给读者带来的是方程的根与函数零点。
二、方程
方程就是一个等式,方程的根就是当方程等于零的时候解出来的根,这个根就叫做方程的根。
求解方程的根的方法是学习作者们掌握的,比如说求解一元二次方程的方法,就有配方法,就是配出完全平方的形式求解,或者是利用十字相乘法求解方程的根。
方程的根再数学界有着明确的定义:
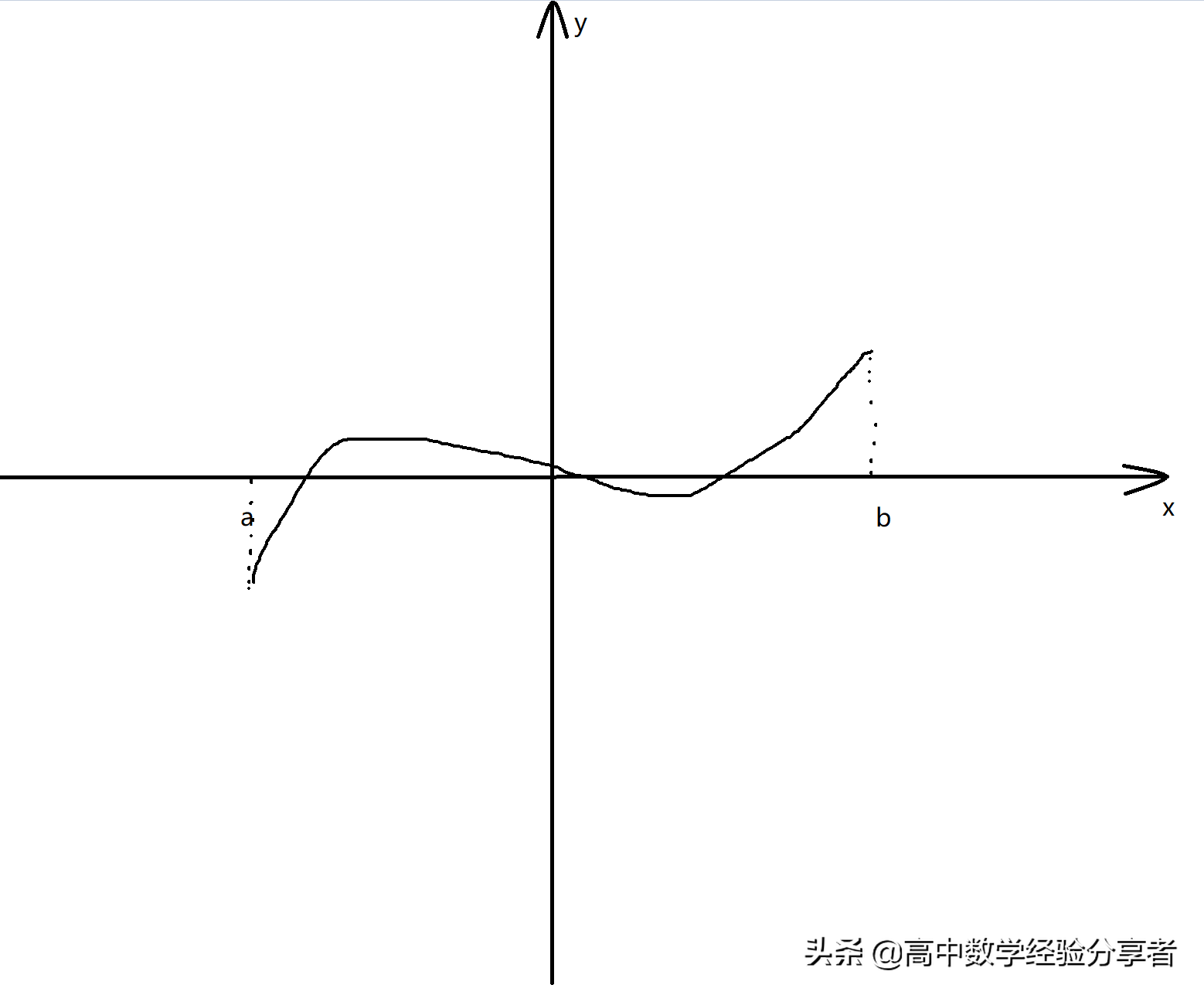
如果函数y = f(x)在区间[a,b]上的图像是连续不断的一条曲线,并且有f(a)*f(b)<0,那么,函数y = f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程 f(x)=0 的根。
画个图更加具体:
三、函数零点
函数零点与方程的根有着相似的形式,都是当方程等于零或者说是函数值f(x)=0的时候,求解出来的x的值,就叫做函数的零点,函数的零点不是点,只是一个自变量。
所以可以得出:
方程y=f(x)有实数根
函数y=f(x)的图像与x轴有交点
函数y=f(x)有零点
批注:
